Как найти площадь параллелограмма
Онлайн калькулятор
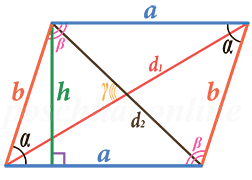
Параллелограмм – это четырёхугольник, у которого противоположные стороны параллельны друг другу.
Узнать чему равна площадь параллелограмма (S) можно зная (либо-либо):
- длину стороны a и длину высоты h
- длины сторон a и b, и угол α
- длины сторон a и b, и угол β
- длины сторон a и b, и длину любой из диагоналей (d1 или d2)
- длины диагоналей d1 и d2, и угол между ними γ
Подставьте значения в соответствующие поля и получите результат.
Зная длину стороны a и длину высоты h
Ответ: S =
Чему равна площадь параллелограмма S если известны длина стороны a и длина высоты h, проведенной к этой стороне?
Формула
S = a⋅h
Пример
Если сторона параллелограмма a = 8 см, а высота h = 4 см, то:
S = 8 ⋅ 4 = 32 см2
Зная длины сторон a и b, и угол α
Ответ: S =
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними α?
Формула
S = a⋅b⋅sinα
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠α = 50° то:
S = 8 ⋅ 5 ⋅ sin 50 = 40 ⋅ 0.766 ≈ 30.64 см2
Зная длины сторон a и b, и угол β
Ответ: S =
Чему равна площадь параллелограмма S если известны длины сторон a и b, и угол между ними β?
Формула
S = a⋅b⋅sin(180 - β)
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а ∠β = 130° то:
S = 8 ⋅ 5 ⋅ sin(180-130) = 40 ⋅ 0.766 ≈ 30.64 см2
Зная длины сторон a и b, и длину диагонали (d1 или d2)
Ответ: S =
Чему равна площадь параллелограмма S если известны длины сторон a и b, и длина любой из диагоналей d?
Формула
S = 2√p⋅(p-a)⋅(p-b)⋅(p-d), где p=(a+b+d)/2
Пример
Если сторона параллелограмма a = 8 см, сторона b = 5 см, а диагональ d = 11 см то:
p = (8 + 5 +11)/2 = 12
S = 2√12⋅(12-8)⋅(12-5)⋅(12-11) = 2⋅√12⋅4⋅7⋅1 = 2⋅√336 = 36.66 см2
Зная длины диагоналей d1 и d2, и угол между ними γ
Ответ: S =
Чему равна площадь параллелограмма S если известны длины диагоналей d1 и d2, и угол между ними γ?
Формула
S = ½⋅d1⋅d2⋅sinγ
Пример
Если диагональ параллелограмма d1 = 11 см, диагональ d2 = 7 см, а ∠γ = 45° то:
S = ½ ⋅ 11 ⋅ 7 ⋅ sin 45 = 38.5 ⋅ 0.7071 ≈ 27.22 см2