Площадь многоугольника

  1. Главная
  2. /
  3. Математика
  4. /
  5. Геометрия
  6. /
  7. Площадь многоугольника
площадь
Чтобы посчитать, площадь правильного многоугольника, воспользуйтесь нашим очень удобным онлайн калькулятором:

Площадь правильного многоугольника

Площадь многоугольника Количество углов (граней) n=
Длина грани a=

Площадь S =
0
Округление ответа:
Просто введите количество граней или углов и длину одной грани, и получите ответ.

Чему равна площадь правильного многоугольника, если известно количество углов n и длина одной из граней a?

Формула

S = n⋅a²4 ⋅ ctg (180n)

Пример №1

К примеру, посчитаем площадь квадрата со стороной 2 см.

Квадрат – это тоже многоугольник, у которого 4 угла.

S = 4⋅2²4 ⋅ ctg (1804) = 4 ⋅ ctg(45) = 4⋅1 = 4 см²

Пример №2

Теперь посчитаем площадь шестиугольника с длиной одной грани в 3 см.

S = 6⋅3²4 ⋅ ctg (1806) = 13.5 ⋅ ctg(30) = 13.5 ⋅ 1.732 = 23.382 см²

Площадь описанного многоугольника

Неправильный многоугольник описанный вокруг окружности =
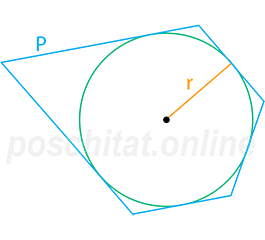Радиус вписанной окружности r =

Площадь S =
0
Округление ответа:

Площадь многоугольника, описанного около окружности, равна половине произведения его периметра P на радиус вписанной окружности r.

Формула

S = ½ ⋅ P ⋅ r

или

S = p ⋅ r

где:

или, если многоугольник правильный:

S = ½ ⋅ n ⋅ a ⋅ r

где:

Пример

Посчитаем площадь пятиугольника с периметром P = 20 см, описанного около окружности с радиусом r = 2.755 см

S = ½ ⋅ 20 ⋅ 2.755 = 10 ⋅ 2.755 = 27.55 см²

Площадь правильного описанного многоугольника

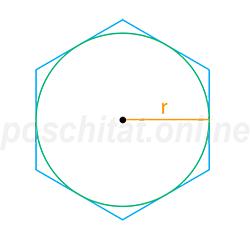Многоугольник описанный вокруг окружности Количество углов (граней) n=
Радиус вписанной окружности r =

Площадь S =
0
Округление ответа:

Площадь правильного многоугольника, описанного около окружности, вычисляется по следующей формуле:

Формула

S = n⋅r²⋅tg (180n)

где:

Пример

Посчитаем площадь правильного шестиугольника с радиусом вписанной окружности r = 3 см.

S = 6⋅3²⋅tg (1806) = 6 ⋅ 9 ⋅ tg30 = 54 ⋅ 0.57735 = 31.1769 см²

Площадь правильного вписанного многоугольника

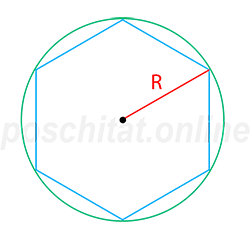Многоугольник вписанный в окружность Количество углов (граней) n=
Радиус описанной окружности R =

Площадь S =
0
Округление ответа:

Площадь правильного многоугольника, вписанного в окружность, вычисляется по следующей формуле:

Формула

S = n⋅R²2 ⋅ sin (360n)

где:

Пример

Посчитаем площадь правильного восьмиугольника с радиусом описанной вокруг его окружности R = 5 см.

S = 8⋅5²2 ⋅ sin (3608) = 100 ⋅ sin45 = 100 ⋅ 0.7071 = 70.71 см²